CLUSTERING WITH R

Today ill show you howto do k-means , k-medoid , Hierarchical and density based clustering in R


K- MEANS CLUSTERING

K-means is one of the simplest unsupervised learning algorithms ,it  aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean. The number of clusters should match the data. An incorrect choice of the number of clusters will invalidate the whole process. An empirical way to find the best number of clusters is to try K-means clustering with different number of clusters and measure the resulting sum of squares.

ADVANTAGES

• Fast, robust and easier to understand.
• Relatively efficient: O(tknd), where n is # objects, k is # clusters, d is # dimension of each object, and t  is # iterations. Normally, k, t, d << n.
• Gives best result when data set are distinct or well separated from each other.

 DISADVANTAGE

• Requires apriori specification of the number of  cluster centers
• If there are two highly overlapping data then k-means will not be able to resolve that there are two clusters.
• Fails for categorical data.
• It uses centroid to represent the cluster therefore unable to handle noisy data and outliers.
• Algorithm fails for non-linear data set.
• It does not work well with clusters (in the original data) of Different size and Different density

Now ill show k-means clustering with Iris dataset.

>data(iris)

>str(iris)

'data.frame':  150 obs. of  5 variables:

 $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...

 $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...

 $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...

 $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...

 $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

We’ll remove the Species from the data as we have mentioned it does not work with categorical data

>iris1=iris[,-5]

>head(iris1)

Sepal.Length Sepal.Width Petal.Length Petal.Width

1          5.1         3.5          1.4         0.2

2          4.9         3.0          1.4         0.2

3          4.7         3.2          1.3         0.2

4          4.6         3.1          1.5         0.2

5          5.0         3.6          1.4         0.2

6          5.4         3.9          1.7         0.4

Now we’ll do clustering with iris1 dataset and use the function kmeans()  for it and will be using 3 clusters

>k_mean=kmeans(iris1,3)

>k_mean

K-means clustering with 3 clusters of sizes 96, 21, 33

Cluster means:

  Sepal.Length Sepal.Width Petal.Length Petal.Width

1     6.314583    2.895833     4.973958   1.7031250

2     4.738095    2.904762     1.790476   0.3523810

3     5.175758    3.624242     1.472727   0.2727273

Clustering vector:

  [1] 3 2 2 2 3 3 3 3 2 2 3 3 2 2 3 3 3 3 3 3 3 3 3 3 2 2 3 3 3 2 2 3 3 3 2 3 3 3 2 3 3 2 2 3 3 2 3 2 3 3 1 1 1 1 1 1

 [57] 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1

[113] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

Within cluster sum of squares by cluster:

[1] 118.651875  17.669524   6.432121

 (between_SS / total_SS =  79.0 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss" "betweenss"    "size"        

[8] "iter"         "ifault"

Now the clustering result is then compared with the class labeled “Species” to check similar objects are grouped together  

>table(iris$Species,k_mean$cluster)

                   1   2    3

  setosa     50   0   0

  versicolor  0 48   2

  virginica    0 14 36

We see that setosa can be easily clustered in one cluster but versicolor and virginica have some amount of overlap. Now we will see graphically .

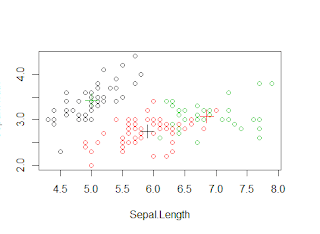
>plot(iris1[c("Sepal.Length", "Sepal.Width")], col = k_mean$cluster)

>points(k_mean$centers[,c("Sepal.Length", "Sepal.Width")], col = 1:3,pch = 3, cex=2)

 We can see that the black dots are separated as one cluster whereas some of the red and green dots are overlapped as we saw in the table for versicolor and virginica.

K- MEDOID CLUSTERING 

K-medoids clustering uses medoids to represent the cluster rather than centroid. A medoid is the most centrally located data object in a cluster.Here, k data objects are selected randomly as medoids to represent k cluster and remaining all data objects are placed in a cluster having medoid nearest (or most similar) to that data object. After processing all data objects, new medoid is determined which can represent cluster in a better way and the entire process is repeated. Again all data objects are bound to the clusters based on the new medoids. In each iteration, medoids change their location step by step.This process is continued until no any medoid move. As a result, k clusters are found representing a set of n data objects.

We ll show k-medoids clustering with functions pam() and pamk().The k-medoids clustering is more robust than k-means in presence of outliers. PAM (Partitioning Around Medoids) is a classic algorithm for k-medoids clustering. While the PAM algorithm is ine cient for clustering large data, the CLARA algorithm is an enhanced technique of PAM by drawing multiple samples of data, applying PAM on each sample and then returning the best clustering. It performs better than PAM on larger

data

We will "fpc" package for this clustering because in this package it  does not require a user to choose k. Instead, it calls the function pam() or clara() to perform a partitioning around medoids clustering with the number of clusters estimated by optimum average

silhouette width.

I have used the same iris data which was used in the k-means clustering

>medoid=pamk(iris1)

>medoid$nc

[1] 2

>table(medoid$pamobject$clustering,iris$Species)

  setosa versicolor virginica

  1     50          1         0

  2      0         49        50

>layout(matrix(c(1,2),1,2))

>plot(medoid$pamobject)

>layout(matrix(1))

We see that it automatically created 2 clusters.Then we check the cluster against the actual Species.The layout function will will help us to see 2 graphs in one screen then we plot the clusters. We see on the left side the 2 clusters one for the setosa and one is the combination of versicolor and verginica and the red line show us the distance between the two cluster.On the right is the silhouette, In the silhouette, a large Si (almost 1) suggests that the corresponding observations are very well clustered, a small Si (around 0) means that the observation lies between two clusters, and observations with a negative Si are probably placed in the wrong cluster. Since the average Si are respectively 0.81 and 0.62 in the above silhouette, the identified two clusters are well clustered. 
You can also specify the no. of cluster if you are sure.


HIERARCHICAL CLUSTERING 

The hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:

• Agglomerative: This is a "bottom up" approach: each observation starts in its own cluster, an pairs of clusters are merged as one moves up the hierarchy.
• Divisive: This is a "top down" approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.

Both this algorithm are exactly reverse of each other.In here ill be covering the Divisive ,the top down approach.

In this example ill use the same iris data.

>hclust=hclust(dist(iris1))

>plot(hclust)

In the above figure we can see that the there we can create 3 clusters , its on us where to cut the line.We can see setosa is easily separated ( in red color box) whereas the vesicolor and verginica are in the next box respectively.

Also we can use first hierarchical clustering to get to know the no.of clusters and then use those no of clusters in the k-means clustering. This is an alternate way to know the k value.


DENSITY - BASED CLUSTERING

The DBSCAN algorithm  from package "fpc" provides a densitybased clustering for numeric data. The idea of density-based clustering is to group objects into one cluster if they are connected to one another by densely populated area. There are two key parameters in DBSCAN :

• ˆ eps: reachability distance, which defines the size of neighbourhood; and
• ˆ MinPts: minimum number of points.

If the number of points in the neighbourhood of point is no less than MinPts, then is a dense point. All the points in its neighbourhood are density-reachable from and are put into the same cluster as alpha.The strengths of density-based clustering are that it can discover clusters with various shapes and sizes and is insensitive to noise. As a comparison, the k-means algorithm tends to find clusters with sphere shape and with similar sizes.

In this again we will use same Iris data 

>densityclus<- dbscan(iris1, eps=0.42, MinPts=5)
>table(densityclus$cluster,iris$Species)

     setosa versicolor virginica

  0      2         10           17

  1     48          0           0

  2      0         37           0

  3      0          3           33  

In the above table, "1" to "3" in the rst column are three identi ed clusters, while "0" stands for noises or outliers, i.e., objects that are not assigned to any clusters. The noises are shown as black circles in the figure below.

>plot(densityclus,iris1)

>plotcluster(iris1, densityclus$cluster)

Again we can see satosa in red marked as 1 is clustered cleanly whereas versicolor and verginica there is some overlap (green "2" and blue "3" colour ).